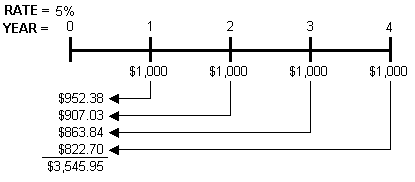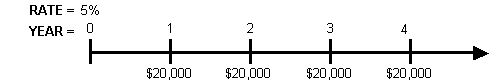Cash Flow Valuation
Introduction
Cash flow valuation is the process of finding the value of money over different time periods. The process is based on the concept of
time value of money, which is one of the most universally useful concepts in finance because the formulas can be used to find the value of any asset where you are expected to receive money in the future, including: bonds, stocks, lottery winnings, structured legal settlements, businesses, and web sites. In order to learn how to value cash flow, you will have to learn other financial concepts. For those who are having calculus flashbacks: don't worry, I'll try to make this as easy as possible. All of the examples below assume you get paid at the end of the year.
Time value of money - "Present value" and "future value"
A dollar in your hand today is worth more than a dollar to be received in the future because if you had it now, you could invest it, earn interest, and end up with more than one dollar in the future. An example would be if you had $100 today and invested it at 5% then you would have $105 in a year. The present value (PV) is $100 and the future value (FV) is $105 and the interest rate (i) would be 5%. Next, I'll show you how to figure out one value when you have the other.
- "Compounding" - finding future value of present cash flow
The process of going from today's value (PV) to tomorrow's value (FV) is called compounding. Expanding on the example above, if someone started with $100 and invested it at 5% and had $105 at the end of year 1, then he could take that $105 and invest it at 5% again and could make an extra $10.25 ($105 times 5%) during year 2 and would have a total of $110.25. Fortunately, you don't have to figure out the profits for each year and add them up, you can figure out the compounded future value by using the following formula:
FV = PV*(1+i)n
where:
FV = future value.
PV = present value.
i = interest rate.
n = number of years.
|
Example: The future value of $5,000 if invested for 7 years at 4% is $6,579.66.
Explanation: $5,000 times (1.04)7=$6,579.66.
- "Discounting" - Finding present values of future cash flow
Finding the present value of an amount of cash you will get in the future is called discounting, and it simply the reverse of compounding. To find the present value, just plug in the future value, interest rate, and number of years into the following formula, which is just an adjusted version of the compounding formula:
Example. The present value of $10,000 received 4 years from now, assuming a rate of 5% would be $8,227.02.
Explanation: ($10,000)/(1.05)4.
Cash Flow Valuation
Now that we learned how to find the present value of a one-time future cash payment, in order to find the present value of a stream of future cash flow, all you have to do is find all of the present values of each individual payment, and then and add up those present values.
How to value cash flow (finite cash flow)
- EVEN CASH FLOW
My first example would be to find the present value of a series of equal payments made for a specific number of years (this is also called an annuity). In the following example you will receive a cash flow of $1,000 for 4 years. To figure out the PV of the $4,000, you will want to take the first year's $1,000 and discount it for 1 year at 5%. Then take the second $1,000 and discount it for 2 years at 5%, etc.
- UNEVEN CASH FLOW
My second example is to find the future value of an uneven cash flow stream. This is called a terminal value. In this example, you will do this the same as the example above - there is no real difference here.
How to value cash flow (infinite cash flow)
You will want to know how to figure out the present value of a cash flow that goes into the future for infinity. This is called a
perpetuity. Theoretically, this is how some stocks (like large, stable companies like GE) are valued because people assume that companies like GE won't ever go out of business so their business is basically an infinite stream of cash flow (their dividends). The further you go into the future each dividend has a smaller present value then the preceding one because it is being discounted more. In fact, if you far enough into the future the present value of the future dividends eventually gets close to zero. Because of this the profits way out in the future actually contribute very little to the present value. When it comes to small and medium companies which you can't assume will be around forever, this formula is still very useful if you assume the company will be profitable for the foreseeable future (10-20 years).
- Infinite cash flow with no growth
Fortunately, when you have an infinite stream of equal cash flows you don't have to add up the present value of all the individual years because the present value of all those future cash flows conveniently equates to the following formula:
|
PV (perpetuity) = Cash flow / interest rate
|
The following example shows how to calculate the present value of a $20,000 annual infinite cash flow.
The present value of the cash flow is equal to $400,000. ($20,000/.05 = $400,000)
- Infinite cash flow with fixed growth
Sometimes you will have an asset whose cash flow and is expected to grow at x% into the future. One example would be a stock of a large company (like Gillette) that is expected to grow at 3% forever. Here the formula for this scenario:
PV = Cash flow / (interest rate - growth rate)
where:
g=constant rate of growth
|
The following example shows an example of a $20,000 annual cash flow that is assumed to grow at a rate of 3% into the future.
The present value of the cash flow is equal to $1,000,000 ($20,000/.05 - .03 = $1,000,000). One restriction of this model is that the growth rate must be lower than the interest rate. If the growth is higher than the interest rate then the results are meaningless.
- Infinite cash flow with uneven growth
The most likely scenario would be that you have a cash flow stream that will have high growth for a few years, but that growth rate will eventually become very low. To figure out the present value you will calculate values of the 2 different parts. The first part is the individual present values of the cash flow during the high-growth years. The second part of the calculation is figuring out the present value of the cash flow stream when the growth declines to a constant number.
The following example shows an example of an annual cash flow that begins at $20,000 for the first year and is assumed to grow at a 20% rate for 2 years. After that, the cash flow will grow 3% each year into for infinity. We then add up all of the calculations. It is easier to look at the graph.
The present value of the cash flow is equal to $1,346,938.78. In this case you can see we calculate the present value of each of the first 3 years and come up with $19,047.62, $21,768.71, and $24,878.52.
The second part of the calculation is the stream of cash flow that begins when the 3% growth rate begins. We then value this portion like we did in the last example - as an infinite cash flow with constant growth. In this case, we take the cash flow for year 4 with a value of $29,664 as the starting point for the infinite cash flow. We then calculate the present value and come up with a value of $1,483,200.00 ($29664/(.05-.03)). Now, this is the value of that infinite cash flow at the beginning of year 4. But we want to find the present value of that cash flow today so we have to discount the $1,483,200.00 further for 3 years at 5%. Therefore, the present value of that $1,483,200.00 3 years from now is $1,281,243.93 (explanation: $1,483,200.00/.05).